Dust Grain Alignment in the Interstellar Medium.

This is a “short” description of a field of study I have been pursuing with my colleagues and students over the last decade or so.   In that time we have had support from various institutions and from the National Science Foundation (NSF) via two three-year grants (Thank you!!).  We are currently grateful to have the support of NSF via award 1715867.

When we observe a star behind a cloud of the interstellar medium (ISM), the light becomes polarized at a few percent.   Just like a pair of polarizing sunglasses allows a fisherman to see where an elusive trout is hiding in a stream, the polarization due to the ISM can uniquely reveal hidden information about the gas, the dust, and the magnetic field in those clouds.

The reason that the light becomes polarized is that some fraction of the dust grains are elongated (whether prolate, like a cigar, or oblate, like a discus, doesn’t matter) and that their long axes line up in the same direction.  When they do, the light is slightly more blocked along the long axis of the grains than along the short axis – and polarization results.

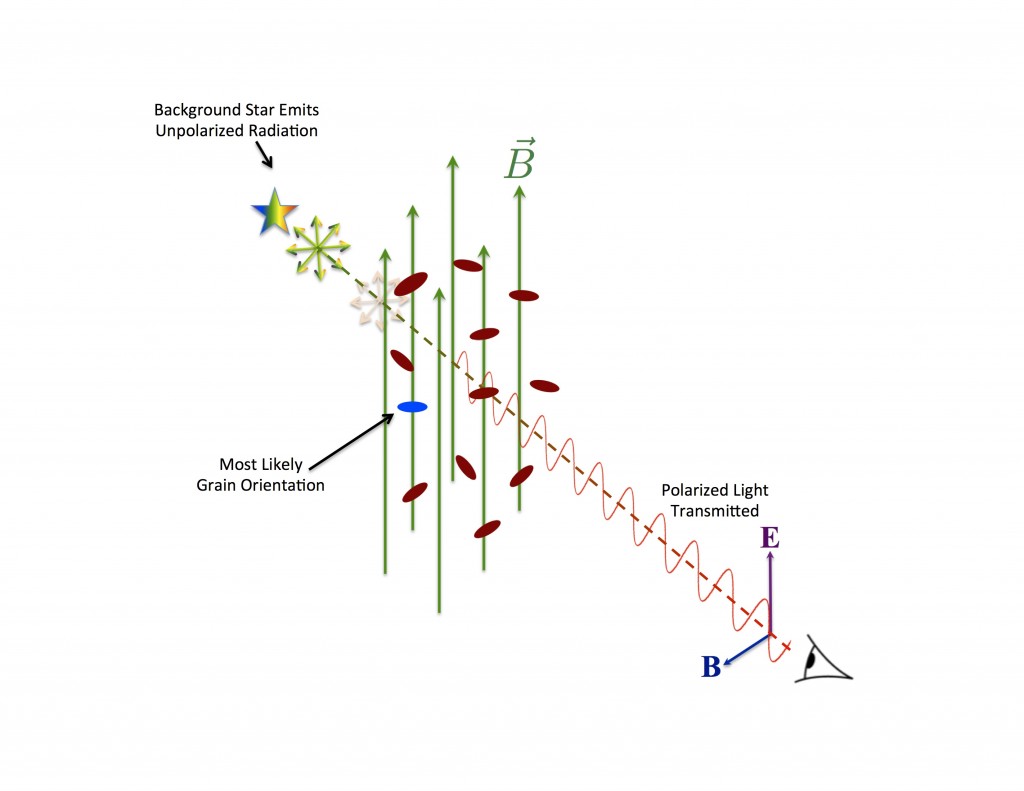
But, how do these grains “know” what direction to line up in?  And, how do they stay aligned in the harsh environment of the ISM?

Already Al Hiltner (of Yerkes Observatory), in his second paper on ISM polarization in 1949, noted that the magnitude of the polarization must be related to the amount of dust on the line of sight [“…a positive color excess is necessary but not sufficient“] and that the direction of the polarization followed the direction of the Galactic magnetic field [“…it appears that the plane of polarization is associated with the galactic plane.”]
Remember; polarization is a [pseudo]vector- it has a magnitude, “p”, and an orientation, “θ”.  It’s a “pseudo vector” since – as opposed to a proper vector – the direction is degenerate on rotation by 180°.  I.e. you can’t tell the difference between “up” and “down”.

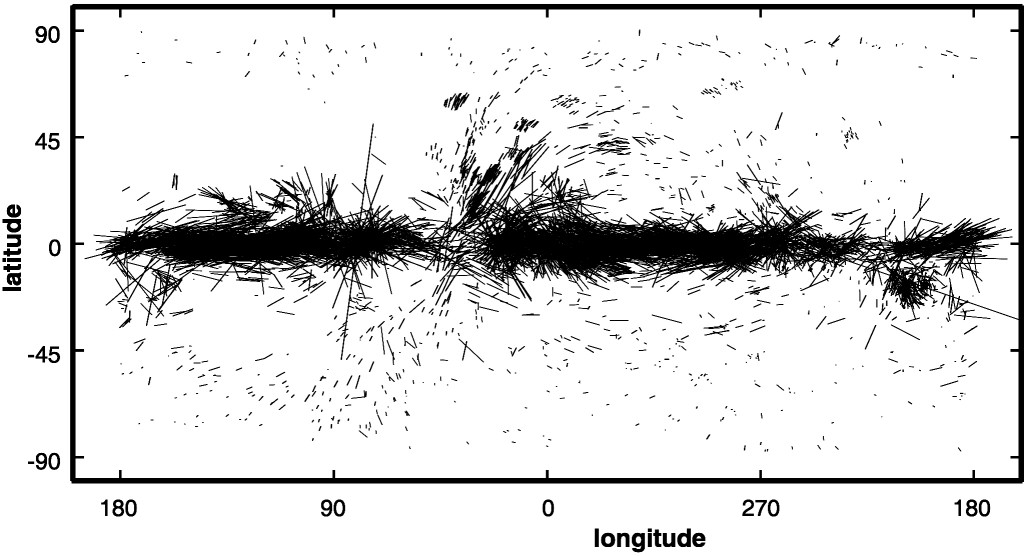
That he was right can be shown, for instance, if one compares the orientation of dust-induced polarization with that due to relativistic electrons orbiting magnetic fields.  Such electrons give rise to synchrotron radiation, which has a characteristic [radio] spectrum, and is very well understood from basic physical principles, so “we know it when we see it”.

As Hiltner noted, however, “…a positive color excess is necessary but not sufficient [to produce polarization]“: Not all line of sight with the same extinction (amount of dust) produce the same level of polarization.  Why is that?

Part of the answer lies in the fact that the grains are rotating (fast) around the magnetic field lines, so if the field is pointing at us, we will not see any polarization.  But that cannot be the whole answer as the polarization can vary a lot over relatively small regions, where it is not reasonable to assume that the orientation of the field varies that much.  Hence a large part of the answer has to come from the mechanism responsible for the grain alignment and how that varies with environment and dust characteristics.

Paramagnetic Dissipation – “Davis-Greenstein” – Alignment

There were several mechanisms proposed for how the grains line up with the magnetic field soon after the discovery of the effect.  The most famous one was proposed by the two Caltech astronomers Leverett Davis Jr. and Jesse Greenstein in 1951, relying on magnetic dissipation inside the grain material.
In a paramagnetic grain (see below) en applied, external, magnetic field makes the grain align its free quantum spins with the applied field causing a magnetization.  However, this effect is not infinitely fast so if the applied field varies faster than the grain material can respond, then instead of an ordered magnetization, energy will be dissipated, a bit like how friction gives rise to heat.  Of course, the ISM magnetic field doesn’t vary on short time scales, but the material inside the grain will experience a rapidly varying external field if the grain rotates fast (in a direction not parallel to the external field).

As shown by R. Victor Jones at Harvard and Lyman Spitzer Jr. at Princeton, in 1967, for this mechanism to work requires that the temperature of the dust and the surrounding gas are significantly different.  The basic argument is as follows:  The lowest energy state of an ensemble  of grain orientations is that they are random.  For a non-random distribution to persist (i.e. aligned grains), there must be a “heat engine” (in a thermodynamic sense) that provides the energy.   Since the mechanism that aligns the grains (in Davis-Greenstein alignment) is inherently a grain material effect (paramagnetic dissipation) but the randomizing effect (gas-grain collisions) is inherently a gas effect, the two systems (gas and dust) must be at different temperatures for DG alignment to work.

Terry Jones showed, already in a paper in 1984, that this was likely not the case.  He showed that while the gas and dust temperatures in “Tapia’s Globule #2” in the Southern Coalsack were the same, distinct polarization could be seen associate with that cloud core.  However the probes of the gas and dust available to him at that time required enough assumptions in their interpretation that the results was not seen as conclusive (or, at least that’s how I interpret the subsequent literature – I was still an undergraduate when that paper came out.  But as I noted about Terry on my page of colleagues, he seems always to have been there first when it comes to polarimetric experiments).

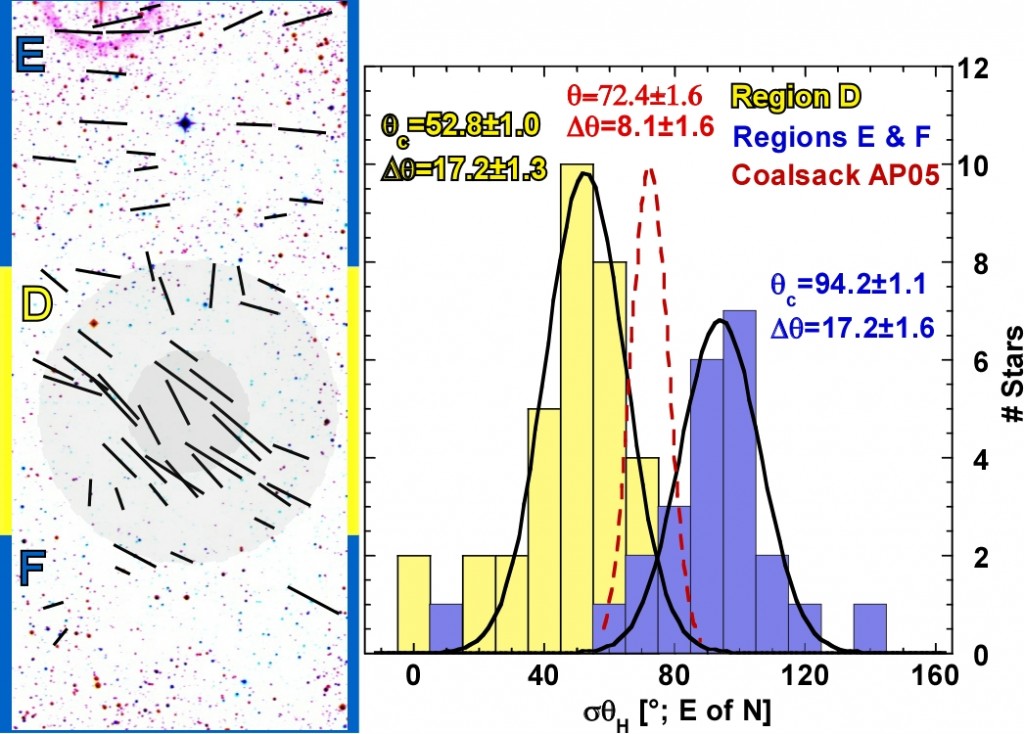
In 2008 Jim Hough at the University of Hertfordshire, UK, performed what many see as the conclusive experiment to address the viability of DG alignment.   He (and his co-authors) observed polarization in the spectral line due to CO ice towards a “true background star” (i.e. the star is far behind the interstellar gas, such that it’s not affecting the material’s physical state).  CO ice can only survive deep into interstellar clouds and so if you see polarization in the associated spectral line, then you know that the grains deep into the cloud are aligned.  Because the dominant heating of the ISM is due to the ultraviolet light, which is very quickly extinguished away from the cloud surfaces, at the depth where CO ice survives the gas and the dust have a common temperature.  Since we see polarization in the CO-ice line that means that DG-mechanism is not what aligns the grains.  So, what does?

Radiative Alignment Torque (RAT) Theory

If a dust grain is irregular, then it will be necessity have a (slightly) helicity – i.e. screw-like twist – in one or the other sense (right, or left hand).  If so, then the right- and left-hand circular polarized components of a radiation field, will scatter off of the grain differently (Remember/note that a general – unpolarized – radiation field can always be decomposed into two orthogonal linear polarized components or a left- and a right-hand polarized component).  Because of this difference in scattering efficiency, when light shines on such a dust grain it starts to rotate.  This idea was originally proposed by the Russian physicists Arkadii Dolginov and Igor Mitrofanov in 1976, but was mostly ignored due to the lack of quantitative predictions.   The proposal was tested numerically in the mid 90ies – by which time computers and codes had “caught up” – by Bruce Draine at Princeton and his then graduate student Joe Weingartner,  for a number of concrete examples of geometric shapes, representing idealized possible grains.  They showed that the torques imparted on the grains were large enough to be able to lead to efficient alignment.

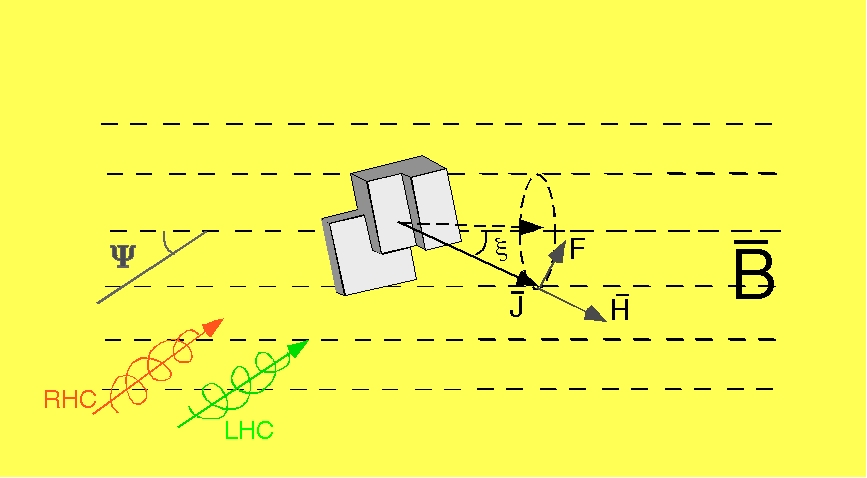
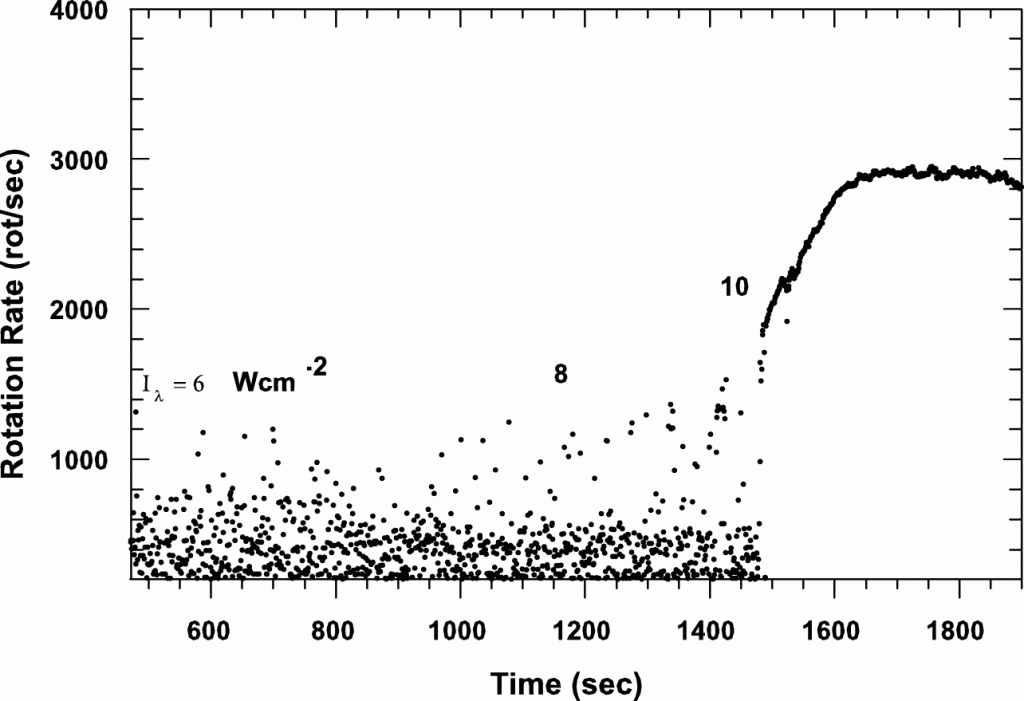
In 2004 Mian Abbas and his group at NASA’s Marshall Space Flight Center used a vacuum system, where they electrostatically suspended SiC grains while illuminating them with a laser.  They could thus show in laboratory experiments that a grain illuminated by a laser, does indeed start to spin, so – experimentally – this works.

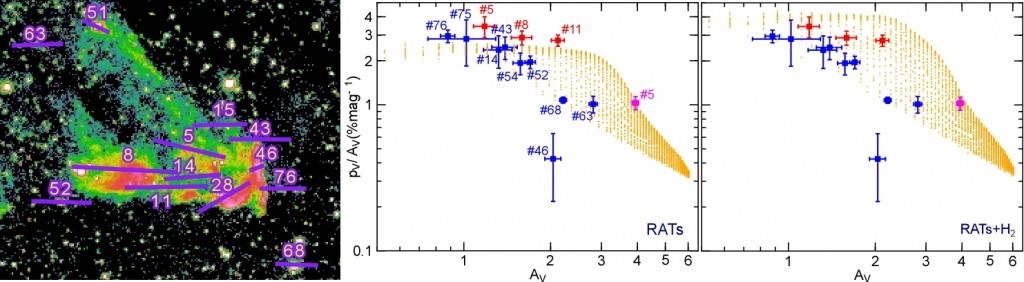
Alex Lazarian and his then graduate student Thiem Hoang in the mid “oughts” (2008) developed a analytical model, which they showed reproduced the numerical “DDSCAT” calculations well.  Because it’s an analytical formulation, much more general question can be asked of such a theory, compared to the numerical modeling, where each configuration has to be calculated individually.  This opened up the possibilities for direct comparisons to observations and specific modeling of observational data sets using ab initio modeling of data (such as the RAT modeling of our IC 63 observations presented in Hoang, Lazarian & Andersson, 2015)

Two kinds of alignment: Internal and External

To give rise to observable polarization, the dust grains have to experience two kinds of alignment.

First each grain has to line up its rotation along one of the grain’s symmetry axes, so that the individual grain shows a time-constant projection.   This is referred to as “internal alignment”.

Then, all the grains (or at least “most of them”) have to align along a common direction in space, so the polarization from all the grains combine to a measurable effect.  This is referred to as “External Alignment”.

Internal Alignment

A grain that gets a “kick” – whether from collisions with a gas particle or from radiative torques – will initially spin around whatever axis that torque is along.   If that is not along one of the grain’s symmetry axes (like in the animation below), the grain will not show a fixed profile and hence not yield (time averaged) polarization.

For a freely rotating grain, the angular momentum (“spin rate”) is a conserved quantity, but the total energy of the grain can change.  It’s relatively easy to show that the lowest energy state of a rotating body (for a fixed angular momentum) is when it’s rotating around its smallest axis (which is the “axis of maximum inertia” – “like so”:).

To turn the grain so that its axis of maximum inertia align with the direction of the angular momentum vector, requires some form of energy internal dispersion (“friction”).

Some of the sources of those internal “frictions” can be  either mechanical plasticity or “Barnett relaxation” (see below – or better; the seminal paper by Edward Purcell in 1979).   Of the two mechanisms, “Barnett relaxation” is much faster.  So for grains that do not experience this effect, the time scale for internal alignment may become significant.  This turns out to be important…

This lining up of the angular momentum and grain symmetry axis is known as “Internal Alignment”.   Once the grains spins around its symmetry axis, its projection is fixed (in space) and so now the single grain can cause polarization

External Alignment
– aligning all the grains with a common direction

A paramagnetic grain (e.g. silicates) – by definition – contains unpaired quantum mechanical spins.  In a grain at rest (and low temperatures) those spins will tend to be equally likely to be oriented “up” and “down”.

Once such a grain starts to rotate, however, then the total energy of the grain can be lowered, while conserving the total angular momentum (as required by conservation laws), if some of the mechanical rotation is traded for spin-flips.  But, of course, if you flip spins out of a distribution with equally many “ups” and “downs” you end up with a net number in one direction.  Since the electron has not only a spin, but an electrical charge and therefore a magnetic moment, if you have a net number of spins in one direction, you also have a net magnetization of the grain.   This is known as the “Barnett effect” (which is the inverse of the “Einstein-de Haas effect” known from laboratory [solid state] physics)

Once the grain acquires a magnetic moment, that magnetization will interact with an external magnetic field, and cause the grain’s spin axis to precess around the direction of the magnetic field (like a wobbly spinning top).  As the radiation illuminates the different faces of the grain as it wobbles, the torques turn the spin axis to coincide with the magnetic field direction.

It should be noted that this is an inherently non-linear process, such that small differences in the initial (starting) conditions, can lead to large differences in the final state.  So, to show what happens to the grains, in detail, you [have to] follow the system as it evolves “in phase space”, starting from many initial conditions and looking at where they end up in a statistical sense.  This is the same process and situation as the “Chaos theory” that was popular in the late 1980ies (“A butterfly flapping its wings in the Amazon can cause a hurricane in New York…”)

As noted above, whereas grains of any composition will (according to RAT theory) be spun up by the radiation, only those made up of paramagnetic materials will align with the magnetic field. However, for strong, and directional enough, radiation fields, grains made up of other materials (such as diamagnetic carbon solids) might instead align with the direction of the light.

We have tested this direct radiative alignment of carbonaceous grains using SOFIA observations of the carbon rich circumstellar envelope of the star IRC+10216 (aka CW Leo), and it works!   I will add some more on this once the paper is finished…

So why should you care?

In summary, we think that now, almost 70 years after the discovery of interstellar polarization, we finally have a self-consistent, observationally supported theory of interstellar grain alignment.   But: “So what”?

First, of course,  solving a long standing research problem is rewarding and good, in and of itself.  Grain alignment is a very rich problem whose solution involves solid body mechanics, solid state (quantum) physics, radiative transfer/scattering, surface physics etc., etc. so it is intellectually stimulating to understand how all those fields of physics come together to explain an astronomical phenomenon.   But there are more direct advantages as well – at least within astronomy.

As has been long recognized, the geometry and local variations in the polarization directions provide a way to measure the magnetic field structure and strength in an interstellar cloud.  So being able to reliably correlate observed polarization to magnetic field geometry will boost our ability to understand this important, but poorly constrained, aspect of the evolution of the ISM, including how, and how efficiently, stars form.

The idea behind how polarization allows us to measure the field strength, is that interstellar magnetic field lines behave like tensed strings (where the tension is proportional to the magnetic field strength).   Just as with e.g. a guitar string, if you loosen the tension the string makes waves of bigger displacement and if you tighten the string it move less.  So by measuring how the string [field line] deviates from a straight line, you can estimate the tension in it [ =magnetic field strength].  This is usually referred to as the Chandrasekhar-Fermi (CF) method, after those two Nobel laureates.  But, as it turns out, Leverett Davis Jr. proposed the idea before the paper by Chandrasekhar and Fermi, even if he didn’t work it out in detail.   Hence, I will side with Prof. Chris McKee in arguing that it should be referred to as the Davis-Chandrasekahr-Fermi (DCF) method.

In addition, if we understand in detail why, how and under what conditions, grains align (with the magnetic field or with strongly directional light), we can use the polarization and it’s wavelength dependence to measure also other environmental condition in the ISM.   How strong is the local high-energy (FUV) radiation field?  How and where do dust grains grow?  What is the mineralogy of the dust grains, and does it vary with environment?  Such diagnostics from polarization, interpreted with a well understood and tested theory, will enhance our understanding of the ISM, star-formation and a number of other areas of astronomy.

That’s what we’re working on now…